leetCode

发表于 更新于 分类于

卡牌分组

给定一副牌，每张牌上都写着一个整数。

此时，你需要选定一个数字 X，使我们可以将整副牌按下述规则分成 1 组或更多组：

每组都有 X 张牌。组内所有的牌上都写着相同的整数。
仅当你可选的 X >= 2 时返回 true。

示例 1：

输入：[1,2,3,4,4,3,2,1]
输出：true
解释：可行的分组是 [1,1]，[2,2]，[3,3]，[4,4]
示例 2：

输入：[1,1,1,2,2,2,3,3]
输出：false
解释：没有满足要求的分组。
示例 3：

输入：[1]
输出：false
解释：没有满足要求的分组。
示例 4：

输入：[1,1]
输出：true
解释：可行的分组是 [1,1]
示例 5：

输入：[1,1,2,2,2,2]
输出：true
解释：可行的分组是 [1,1]，[2,2]，[2,2]

涉及点

  • 辗转相除法 求最大公约数
  • 利用哈希表计算元素出现次数

自己的解答

  • 首先利用 ES6 新数据结构 Map ，计算元素出现的次数
  • 使用...运算符将其转为数组，不要忘记利用 (Map.protype.values()返回的是一个新的Iterator对象)
  • 然后遍历数组，取当前项与后一项做辗转相除法，求出最大公约数后赋值给后一项，直到运算完成
  • 这里需要考虑[1,1]的这种情况，由于次数数组程度为 1 ，所以做了特殊处理
  • 然后只要判断最后的最大公约数是否大于 2 即可
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
var hasGroupsSizeX = function(deck) {
  if(deck.length<2){
    return false
  }
  const countMap = new Map()
  for (let i = 0; i < deck.length; i++) {
    countMap.set(deck[i],countMap.has(deck[i]) ? countMap.get(deck[i]) + 1 : 1)
  }
  const countArray = [...countMap.values()] 
  console.log(countArray);
  let g;
  if(countArray.length === 1 && countArray[2] >=2 ){
    return true
  }
  for (let i = 0; i < countArray.length - 1; i++) {
    g = ojld(countArray[i], countArray[i+1])
    countArray[i+1] = g
  }
  return g >= 2
};
function ojld(chushu, yushu) {
  if(chushu % yushu === 0){
    return yushu
  }else{
    return ojld(yushu, chushu % yushu)
  }
}

网上的解答,在此仅展示部分代码，代码取第一位做了一次重复运算，所有不需要考虑特殊情况

1
2
3
4
5
6
7
8
9
10
11
/*
最大公约数
因为该数组是出现次数数组，最小值至少为1（至少出现1次），所以默认赋值为数组首位对公约数计算无干扰
*/
let g = timeAry[0];

// 遍历出现次数，计算最大公约数
timeAry.forEach(time => {
  // 因为需要比较所有牌出现次数的最大公约数，故需要一个中间值
  g = gcd(g, time);
});

605 种花问题

假设你有一个很长的花坛，一部分地块种植了花，另一部分却没有。可是，花卉不能种植在相邻的地块上，它们会争夺水源，两者都会死去。

给定一个花坛（表示为一个数组包含0和1，其中0表示没种植花，1表示种植了花），和一个数 n 。能否在不打破种植规则的情况下种入 n 朵花？能则返回True，不能则返回False。

示例 1:
输入: flowerbed = [1,0,0,0,1], n = 1
输出: True

示例 2:
输入: flowerbed = [1,0,0,0,1], n = 2
输出: False

注意:

  • 数组内已种好的花不会违反种植规则。
  • 输入的数组长度范围为 [1, 20000]。
  • n 是非负整数，且不会超过输入数组的大小。

官方解答, 有几个缺点

  • 边界条件过于负责
  • 遍历次数较多
1
2
3
4
5
6
7
8
9
10
11
12
13
var canPlaceFlowers = function(flowerbed, n) {
  let count = 0
  for (let i = 0,length = flowerbed.length; i < length; i++) {
    const item = flowerbed[i];
    if(item!=1){
      if((i==0||flowerbed[i-1]==0)&&(i==flowerbed.length-1||flowerbed[i+1]==0)){
        flowerbed[i] = 1
        count++
      }
    }
  }
  return count>=n
};

较好的解答, 通俗易懂

  • 两边不为1，隐含着最左和最右的边界条件
  • 当符合种花条件时，将遍历序号 +1 取代赋值，减少了遍历次数
1
2
3
4
5
6
7
8
9
10
var canPlaceFlowers = function (flowerbed, n) {
  var num = 0
  for (var i = 0, length = flowerbed.length; i < length; i++) {
    if (flowerbed[i] === 0 && flowerbed[i - 1] !== 1 && flowerbed[i + 1] !== 1) {
      num++
      i++
    }
  }
  return n <= num
};

格雷编码

优秀解题思路-附带图解
主要就是找规律，据说数字电路课有讲解

我的解答

1

84 柱状图中最大的矩形

给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。

求在该柱状图中，能够勾勒出来的矩形的最大面积。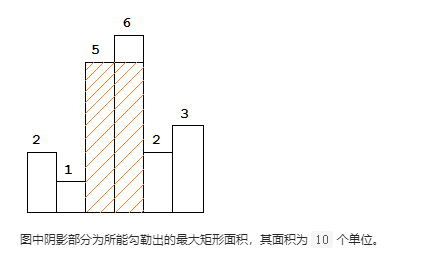
最大矩形

我的解法，用最原始的方法进行解答，理论上可行，但是空间复杂度和时间复杂度太复杂了

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
var largestRectangleArea = function(heights) {
  let maxArea = 0
  while (heights.length !== 0) {
    const lengths = [...heights];
    while(lengths.length !== 0){
      let area = Math.min(...lengths) * lengths.length
      if(area>maxArea){
        maxArea = area
      }
      lengths.pop()
    }
    heights.shift()
  }
  return maxArea
};

单调栈应用优秀讲解 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
const largestRectangleArea = (heights) => {
  let maxArea = 0
  const stack = []
  heights = [0, ...heights, 0]         
  for (let i = 0; i < heights.length; i++) { 
    while (heights[i] < heights[stack[stack.length - 1]]) { // 当前bar比栈顶bar矮
      const stackTopIndex = stack.pop() // 栈顶元素出栈，并保存栈顶bar的索引
      maxArea = Math.max(               // 计算面积，并挑战最大面积
        maxArea,                        // 计算出栈的bar形成的长方形面积
        heights[stackTopIndex] * (i - stack[stack.length - 1] - 1)
      )
    }
    stack.push(i)                       // 当前bar比栈顶bar高了，入栈
  }
  return maxArea
}

面试中遇到的算法题 两个有序数组合并为一个有序数组

两个数组
let arr1 = [0, 3, 5, 8, 15, 19]
let arr2 = [1, 2, 7, 13, 16, 17, 18]
结果输出为
[0, 1, 2, 3, 5, 7, 8, 13, 15, 16, 17, 18]
假设两个数组都为升序排列 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
let arr1  = [-1, 0, 1, 5, 8, 15, 19, 22, 33]
let arr2 =  [3, 4, 7, 13, 15, 16, 17, 18, 19, 20, 33, 34, 35]
for (let i = 0; i < arr1.length; i++) {
  for (let j = 0; j < arr2.length; j++) {
    if(arr1[i]<arr2[j]){
      arr2.splice(j, 0, arr1[i]);
      break;
    }else if(j === arr2.length -1){
      arr2.splice(j + 1, 0, arr1[i]);
    }
  }
}
```  

引申，如果不让使用for循环、sort  
**下边这个方法问题不大，测试了很多数据，还拥有优化空间**

let arr1 = [-1, 0, 1, 5, 8, 15, 19, 22, 33]
let arr2 = [3, 4, 7, 13, 15, 16, 17, 18, 19, 20, 33, 34, 35]
function handle(arr1, arr2) {
if(arr1.length === 0){
return
}else{
var v1 = arr1.shift()
addPosition(v1, arr2, 0)
return handle(arr1, arr2)
}
}
function addPosition(v1, arr2, index){
if(index >= arr2.length){
return
}else{
if(v1 <= arr2[index] && (index === 0 || v1 > arr2[index - 1])){
arr2.splice(index, 0, v1)
return
} else if(index === arr2.length - 1) {
if(v1 > arr2[index]){
arr2.splice(index + 1, 0, v1)
return
}
}
return addPosition(v1, arr2, index + 1)
}
}
handle(arr1, arr2)
console.log(arr2);

1
2
3
4

***
其实升序排列 还隐藏着一些条件，上述代码优化如下

let arr1 = [-1, 0, 1, 5, 8, 15, 19, 22, 33]
let arr2 = [3, 4, 7, 13, 15, 16, 17, 18, 19, 20, 33, 34, 35]
function handle(arr1, arr2) {
if(arr1.length === 0){
return
}else{
var v1 = arr1.shift()
addPosition(v1, arr2, 0)
return handle(arr1, arr2)
}
}
function addPosition(v1, arr2, index){
if(index >= arr2.length){
return
}else{
// 优化了下列代码
if(v1 <= arr2[index]){
arr2.splice(index, 0, v1)
return
} else if(index === arr2.length - 1) {
arr2.splice(index + 1, 0, v1)
return
}
// 优化结束
return addPosition(v1, arr2, index + 1)
}
}
handle(arr1, arr2)
console.log(arr2);