简单记录学习极客时间-数据与结构之美-排序相关的知识记录
tips 排序动画演示 可用手机app
时间复杂度 On2 冒泡排序 冒泡排序只会操作相邻的两个数据。每次冒泡操作都会对相邻的两个元素进行比较，看是否 满足大小关系要求。如果不满足就让它俩互换。一次冒泡会让至少一个元素移动到它应该在 的位置，重复 n 次，就完成了 n 个数据的排序工作。
冒泡排序最不容易出错。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 const arr = [4,5,2,3,8,7,6,1,10] function bubble(arr) { const l = arr.length for (let i = 0; i < l - 1; i++) { // 没有交换发生 其实代表数组已经是有序的了 let flag = true; for (let j = i + 1; j < arr.length; j++) { if (arr[i] > arr[j]) { const temp = arr[i] arr[i] = arr[j] arr[j] = temp // 有交换发生 flag = false; } } if (flag) { break; } } } bubble(arr) console.log(arr);
插入排序 首先，我们将数组中的数据分为两个区间，已排序区间和未排序区间。初始已排序区间只有 一个元素，就是数组的第一个元素。插入算法的核心思想是取未排序区间中的元素，在已排 序区间中找到合适的插入位置将其插入，并保证已排序区间数据一直有序。重复这个过程， 直到未排序区间中元素为空，算法结束。
插入排序写起来比较费劲，要注意的地方比较多
我自己的写的
1 2 3 4 5 6 7 8 9 10 11 12 13 function insert(arr) { const l = arr.length for (let i = 0; i < l - 1; i++) { let j = i + 1 while (arr[j-1] > arr[j] && j>=0) { const temp = arr[j] arr[j] = arr[j-1] arr[j-1] = temp j-- } } } insert(arr)
教程写的，已经换成JavaScript，并加了注释
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 function insert2(arr) { const l = arr.length; for (let i = 1; i < l; ++i) { // 缓存当前处理的元素，减少交换次数 let value = arr[i]; // 对比前方排序区，查找插入的位置 let j = i - 1; for ( ; j >= 0; --j) { if (arr[j] > value) { // 相当于把arr[j]向右移一位 // 第一次被覆盖掉的元素是当前处理元素，已在顶部缓存 // 第一次以后被覆盖的元素，实际上已经保存在右侧了 arr[j + 1] = arr[j]; // 数据移动 } else { // 当前元素已经满足条件，不需要交换 break; } } // 只在最后交换 j+1 arr[j + 1] = value; // 插入数据 } }
选择排序 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 function select(arr) { const l = arr.length let min, minIndex for (let i = 0; i < l - 1; i++) { // 起始位置 min = arr[i] minIndex = i for (let j = i+1; j < l; j++) { if (arr[j] < min) { min = arr[j] minIndex = j } } const temp = arr[i] arr[i] = min arr[minIndex] = temp } } // select(arr) console.log(arr);
时间复杂度 O nlogn 归并排序(稳定) 自己的代码，未优化的版本，找了好久的错误
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 // 归并排序 function merginInto(arr, l, r) { if (l === r) { return arr } const m = (l + r) >> 1 // 相当于除以2 取整 const left = arr.slice(l, m + 1) const right = arr.slice(m + 1, r + 1) return sortOrderArr( left.length <= 1 ? left: merginInto( // 忘了把边界改成新数组的了 left, 0, m ), right.length <= 1 ? right : merginInto( // 忘了把边界改成新数组的了 right, 0, r - (m + 1) ) ) } // 将两个有序数组合并 function sortOrderArr(arr1, arr2) { const res = [] let i1 = i2 = 0, l1 = arr1.length, l2 = arr2.length while (i1<l1 || i2<l2) { if (i1 === l1) { res.push(arr2[i2++]) } else if(i2===l2) { res.push(arr1[i1++]) }else if (arr1[i1] <= arr2[i2]) { res.push(arr1[i1++]) }else( res.push(arr2[i2++]) ) } return res }
比较大众的写法，这个类似于二叉树的后续遍历
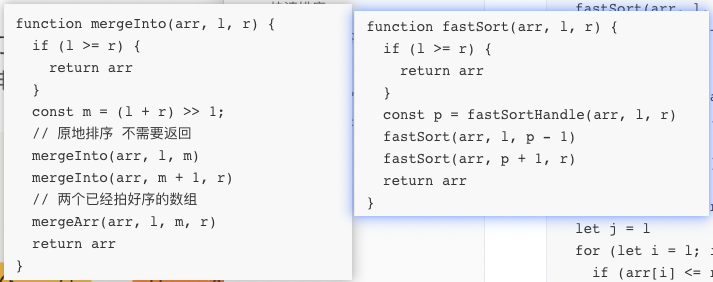
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 function mergeInto(arr, l, r) { if (l >= r) { return arr } const m = (l + r) >> 1; // 原地排序 不需要返回 mergeInto(arr, l, m) mergeInto(arr, m + 1, r) // 两个已经拍好序的数组 mergeArr(arr, l, m, r) return arr } function mergeArr(arr, l, m, r) { const res = [] let i1 = l, i2 = m + 1, l1 = m+1, l2 = r+1 while (i1<l1 || i2<l2) { if (i1 === l1) { res.push(arr[i2++]) } else if(i2===l2) { res.push(arr[i1++]) }else if (arr[i1] <= arr[i2]) { res.push(arr[i1++]) }else( res.push(arr[i2++]) ) } for (let i = l,j=0; i < r+1; i++,j++) { arr[i] = res[j] } }
快速排序(不稳定) 把比参考位置小的数移到左侧，大的移到右侧，如果不额外占用空间的话，比较难写
空间复杂度 O n 比较容易写出来
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 function fastSort(arr, l, r) { if (l >= r) { return arr } const p = fastSortHandle(arr, l, r) fastSort(arr, l, p - 1) fastSort(arr, p + 1, r) return arr } // 快排辅助函数 分区 排序 function fastSortHandle(arr, l, r) { // 占用了 On的空间 const res = [] //随机会好一点 const rdm = Math.floor(Math.random()*(r-l+1)+l) const ref = arr[rdm] let li = l, ri = r for (let i = l; i < r + 1; i++) { if (i === rdm) { continue } if (arr[i] <= ref) { res[li] = arr[i] li++ } else { res[ri] = arr[i] ri-- } } res[ri] = ref for (let i = l; i < r+1; i++) { arr[i] = res[i] } return ri }
O1空间复杂度左右归类的算法解释 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 function fastSortHandle(arr, l, r) { // const rdm = Math.floor(Math.random()*(r-l+1)+l) const rdm = 1 const ref = arr[rdm] let j = l for (let i = l; i < r + 1; i++) { // 跳过 if (i === rdm) { continue; } // 跳过 if (j === rdm) { j++ } if (arr[i] <= ref) { [arr[i], arr[j]] = [arr[j], arr[i]] j++ } } if (rdm < j) { j-- } [arr[rdm], arr[j]] = [arr[j], arr[rdm]] return j }
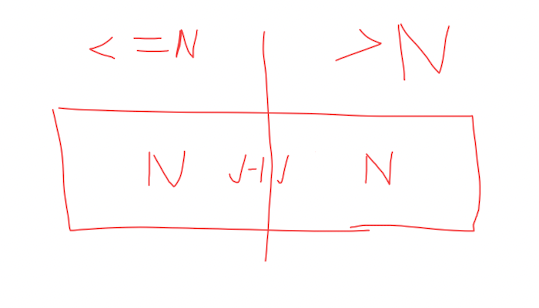
当选择一个随机数N，下标INDEX作为参照点的话，程序运行到关键点的情况应该如下图所示
左侧是小于等于N的数，右侧是大于N的数，但是N可能在左侧或者右侧
最好的情况就是 把N的位置放进 j-1 和 j之间，但是这样时间复杂度较高，采取交换替代
如果N在左侧就和J-1交换，N在右侧就和J置换，如果不需要随机选择位置的话，N取最右侧元素，就不需要判断了
1 2 3 4 5 6 if (rdm < j) { j-- } [arr[rdm], arr[j]] = [arr[j], arr[rdm]] return j
更好的随机数左右归类 力扣官方 采取先用随机数与最后一位交换位置在进行常规方法，方法容易理解，也不容易出错
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 int partition(vector<int>& nums, int l, int r) { int pivot = nums[r]; int i = l - 1; for (int j = l; j <= r - 1; ++j) { if (nums[j] <= pivot) { i = i + 1; swap(nums[i], nums[j]); } } swap(nums[i + 1], nums[r]); return i + 1; } int randomized_partition(vector<int>& nums, int l, int r) { int i = rand() % (r - l + 1) + l; // 随机选一个作为我们的主元 swap(nums[r], nums[i]); return partition(nums, l, r); }
最后总结出JavaScript版本的快速排序
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 function fastSort(arr, l, r) { if (l >= r) { return arr } const p = fastSortHandle(arr, l, r) // -1 +1 可别忘 会死循环的 fastSort(arr, l, p - 1) fastSort(arr, p + 1, r) return arr } function fastSortHandle(arr, l, r) { const rdm = Math.floor(Math.random() * (r - l + 1) + l) // 与最后元素交换 swap(arr, rdm, r) const ref = arr[r] let j = l for (let i = l; i < r; i++) { if (arr[i] <= ref) { swap(arr, i, j) j++ } } swap(arr, r, j) return j } function swap(arr, p, q) { const temp = arr[p] arr[p] = arr[q] arr[q] = temp }
归并排序和快速排序的区别与联系
快排和归并用的都是分治思想，递推公式和递归代码也非常相似，那它们的区别在哪里呢?
而快排正好相反，它的处理过程是由上到下的，先分区，然后再处理子问题。
归并排序虽然是稳定的、时 间复杂度为 O(nlogn) 的排序算法，但是它是非原地排序算法。我们前面讲过，归并之所以 是非原地排序算法，主要原因是合并函数无法在原地执行。快速排序通过设计巧妙的原地分区函数，可以实现原地排序，解决了归并排序占用太多内存的问题。
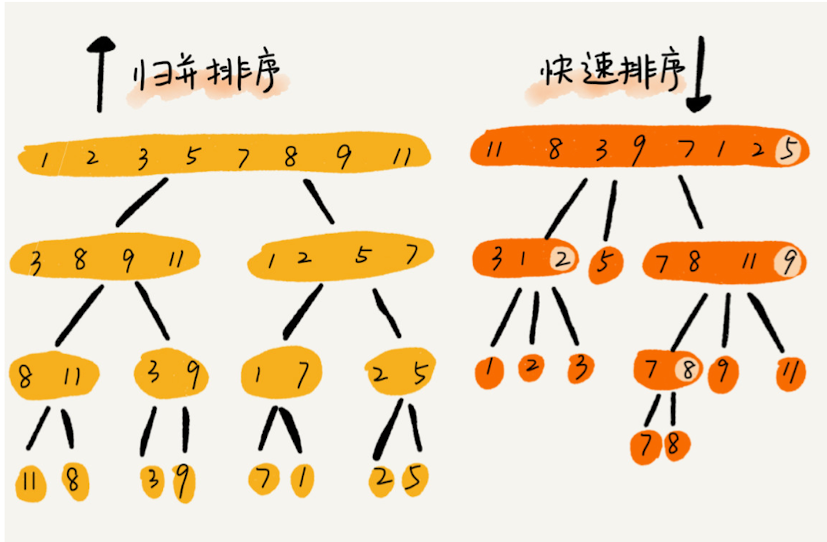可以发现，归并排序的处理过程是由下到上的，先处理子问题，然后再合并。