二叉树遍历

发表于 分类于 ，

常规遍历

优秀题解

递归

递归的代码很简单

前序 中左右

这种写法其实不好，容易让人误解，return res 会被执行好多次

1
2
3
4
5
6
7
8
9
var preorderTraversal = function(root, res = []) {
  if(!root){
    return res
  }
  res.push(root.val)
  preorderTraversal(root.left, res)
  preorderTraversal(root.right, res)
  return res
};

下面这种容易理解

1
2
3
4
5
6
7
8
9
10
11
12
13
var preorderTraversal = function(root) {
 var res = []
  if(!root){
    return res
  }
  res.push(root.val)
  preorderTraversal(root.left, res)
  preorderTraversal(root.right, res)
  return res
};
function handle(root) {

}

中序 左中右

1
2
3
4
5
6
7
8
9
var preorderTraversal = function(root, res = []) {
  if(!root){
    return res
  }
  preorderTraversal(root.left, res)
  res.push(root.val)
  preorderTraversal(root.right, res)
  return res
};

后序 左右中

1
2
3
4
5
6
7
8
9
var preorderTraversal = function(root, res = []) {
  if(!root){
    return res
  }
  preorderTraversal(root.left, res)
  preorderTraversal(root.right, res)
  res.push(root.val)
  return res
};

迭代

迭代的很不容易理解

前序 中左右

普通写法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
var preorderTraversal = function(root) {
  if(!root){
    return []
  }
  const stack = [];
  const res = []
  stack.push(root)
  while(stack.length){
    const popNode = stack.pop()
    res.push(popNode.val)
    if(popNode.right){
      stack.push(popNode.right)
    }
    if(popNode.left){
      stack.push(popNode.left)
    }
  }
  return res
};

统一写法 前序和中序 结果采集的地方不同，一个是出栈 一个是入栈

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
var preorderTraversal = function(root) {
  const res = []
  let cur = root
  const stack = []
  while (stack.length || cur) {
    while (cur) {
      res.push(cur.val)
      stack.push(cur)
      cur = cur.left
    }
    const popNode = stack.pop()
    if(popNode.right){
      cur = popNode.right
    }
  }
  return res
};

中序 左中右

统一写法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
var inorderTraversal = (root) => {
  const res = []
  let cur = root
  const stack = []
  while (stack.length || cur) {
    // 找到最左侧的节点，并把沿路的节点全部推入栈中
    while(cur){
      stack.push(cur)
      cur = cur.left
    }
    // 取出栈顶元素
    const popNode = stack.pop()
    // 记录出栈元素
    res.push(popNode.val)
    // 存在右节点 即为父节点 而且左节点已经处理过了
    if(popNode.right){
      cur = popNode.right
    }
  }
  return res
};

后序 左右中

可以把前序的普通写法改一下，变成中右左，然后倒着输出

普通写法倒着输出

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
const postorderTraversal = function(root) {
  const res = []
  if(!root){
    return res
  }
  const stack = []
  stack.push(root)
  while(stack.length){
    const popRoot = stack.pop()
    res.push(popRoot.val)
    // 左右换一下顺序
    if(popRoot.left){
      stack.push(popRoot.left)
    }
    if(popRoot.right){
      stack.push(popRoot.right)
    }
  }
  // 倒着输出
  return res.reverse()
};

统一写法倒着输出

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
const postorderTraversal = function(root) {
  const res = []
  let cur = root
  const stack = []
  while (stack.length || cur) {
    while (cur) {
      res.push(cur.val)
      stack.push(cur)
      cur = cur.right
    }
    const popNode = stack.pop()
    if(popNode.left){
      cur = popNode.left
    }
  }
  // 把上边的push 换成unshift 这边就不用倒着了 但是时间复杂度更高了，不好
  return res.reverse()
};

利用标识符进行迭代,普通写法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
const postorderTraversal = function(root) {
  if (!root) {
    return []
  }
  const stack = []
  const res = []
  stack.push({
    node: root,
    flag: 0
  })
  while (stack.length) {
    const {node, flag} = stack.pop()
    if (!node) {
      continue
    }
    if (flag === 1) {
      res.push(node.val)
    } else {
      stack.push({
        node: node,
        flag: 1
      })
      stack.push({
        node: node.right,
        flag: 0
      })
      stack.push({
        node: node.left,
        flag: 0
      })
    }
  }
  return res
};

优秀统一迭代法 直接记这个就好

前序遍历统一迭代法

// 前序遍历：中左右
// 压栈顺序：右左中

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
var preorderTraversal = function(root, res = []) {
    const stack = [];
    if (root) stack.push(root);
    while(stack.length) {
        const node = stack.pop();
        if(!node) {
            res.push(stack.pop().val);
            continue;
        }
        if (node.right) stack.push(node.right); // 右
        if (node.left) stack.push(node.left); // 左
        stack.push(node); // 中
        stack.push(null);
    };
    return res;
};

中序遍历统一迭代法

// 中序遍历：左中右
// 压栈顺序：右中左

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
var inorderTraversal = function(root, res = []) {
    const stack = [];
    if (root) stack.push(root);
    while(stack.length) {
        const node = stack.pop();
        if(!node) {
            res.push(stack.pop().val);
            continue;
        }
        if (node.right) stack.push(node.right); // 右
        stack.push(node); // 中
        stack.push(null);
        if (node.left) stack.push(node.left); // 左
    };
    return res;
};

后序遍历统一迭代法

// 后续遍历：左右中
// 压栈顺序：中右左

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
var postorderTraversal = function(root, res = []) {
    const stack = [];
    if (root) stack.push(root);
    while(stack.length) {
        const node = stack.pop();
        if(!node) {
            res.push(stack.pop().val);
            continue;
        }
        stack.push(node); // 中
        stack.push(null);
        if (node.right) stack.push(node.right); // 右
        if (node.left) stack.push(node.left); // 左
    };
    return res;
};

作者：carlsun-2
链接：https://leetcode-cn.com/problems/binary-tree-preorder-traversal/solution/dai-ma-sui-xiang-lu-chi-tou-qian-zhong-hou-xu-de-d/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

层序遍历

leetcode一道基础的题

102. 二叉树的层序遍历

难度中等1081收藏分享切换为英文接收动态反馈

给你一个二叉树，请你返回其按 层序遍历 得到的节点值。 （即逐层地，从左到右访问所有节点）。

示例：
二叉树：[3,9,20,null,null,15,7],

1
2
3
4
5
  3
 / \
9  20
  /  \
 15   7

返回其层序遍历结果：

1
2
3
4
5
[
  [3],
  [9,20],
  [15,7]
]

递归解法

利用层级和数组解决

1
2
3
4
5
6
7
8
9
10
11
12
13
14
var levelOrder = function(root) {
  const levelArr = []
  handle(root,0,levelArr)
  return levelArr
};
function handle(root, level, levelArr){
  if(!root){
    return
  }
  Array.isArray(levelArr[level]) ? levelArr[level].push(root.val) : levelArr[level] = [root.val]
  level++
  handle(root.left, level, levelArr)
  handle(root.right, level, levelArr)
}

迭代解法

方法看一下 很容易就能理解

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
var levelOrder = function(root) {
  const res = []
  if(!root){
    return res
  }
  const queue = [root]
  let index = 0
  while (queue.length) { // 关键点
    // 每一层的新开始
    // 记录当前层的节点个数，防止shift多了
    const l = queue.length // 关键点
    res.push([])
    // 把该层推入结果，顺便把该层的下一层推入q中
    for(var i=0;i<l;i++){ // 关键点
      const head = queue.shift()
      res[index].push(head.val)
      if(head.left){
        queue.push(head.left)
      }
      if(head.right){
        queue.push(head.right)
      }
    }
    index++
  }
  return res
};

加深对二叉树递归的理解

230. 二叉搜索树中第K小的元素 labuladong 题解 思路

给定一个二叉搜索树的根节点 root ，和一个整数 k ，请你设计一个算法查找其中第 k 个最小元素（从 1 开始计数）。

示例 1：

img

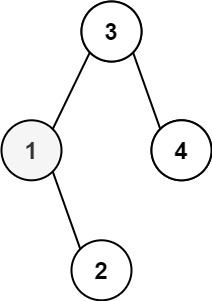
1
2
输入：root = [3,1,4,null,2], k = 1
输出：1

示例 2：

img

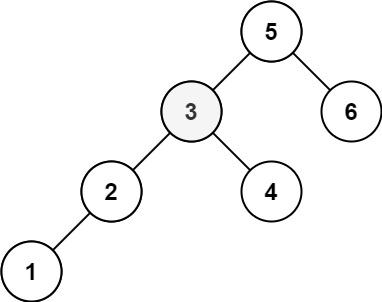
1
2
输入：root = [5,3,6,2,4,null,null,1], k = 3
输出：3

对递归理解不深的解法，没错 我写的

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
var kthSmallest = function(root, k) {
  let res
  function handle(root, count, k){
    if(!root){
      return
    }
    handle(root.left, count, k)
    if(count === k){
      res = root.val
      return
    }
    count++
    handle(root.right, count, k)
  }
  handle(root, 1, k)
  return res
};

实际上的正确解法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
var kthSmallest = function(root, k) {
  let count = 1
  function handle(root, k){
    if(!root){
      return
    }
    handle(root.left, k)
    if(count === k){
      res = root.val
      // 如果没有这个count++ 会一直指向下一个节点
      count++
      return
    }
    count++
    handle(root.right, k)
  }
  handle(root, k)
  return res
};

搜索二叉树插入数据

重点理解两种模式的不同

我的解法 简单直接

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
var insertIntoBST = function(root, val) {
  if(!root){
    return new TreeNode(val)
  }
  if(val > root.val){
    if(!root.right){
      root.right = new TreeNode(val)
    }else{
      insertIntoBST(root.right, val)
    }
  }else{
    if(!root.left){
      root.left = new TreeNode(val)
    }else{
      insertIntoBST(root.left, val)
    }
  }
  return root
};

另一种解法 不太容易理解

1
2
3
4
5
6
7
8
9
10
11
12
13
var insertIntoBST = function(root, val) {
  if(!root){
    return new TreeNode(val)
  }
  if(val > root.val){
    root.right = insertIntoBST(root.right, val)
  }else{
    root.left = insertIntoBST(root.left, val)
  }
  // 对return之外情况的兜底 找不到原样返回
  // root.right = root.right
  return root
};

搜索二叉树的删除操作

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
var deleteNode = function(root, key) {
  if(!root){
    return root
  }
  if(root.val === key){
    if(!root.left){
      // 如果root.right 也不存在 就是null
      return root.right
    }
    if(!root.right){
      return root.left
    }
    const minVal = getRightMin(root.right)
    root.val = minVal.val
    root.right = deleteNode(root.right, minVal.val)
  }else if(key < root.val){
    root.left = deleteNode(root.left, key)
  }else{
    root.right = deleteNode(root.right, key)
  }
  return root
};
function getRightMin(root){
  while(root.left){
    root = root.left
  }
  return root
}

95. 不同的二叉搜索树 II

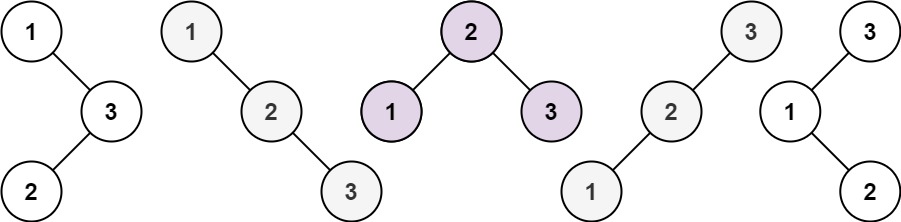
给你一个整数 n ，请你生成并返回所有由 n 个节点组成且节点值从 1 到 n 互不相同的不同 二叉搜索树 。可以按 任意顺序 返回答案。

img

示例 1：

1
2
3
输入：n = 3
输出：[[1,null,2,null,3],[1,null,3,2],[2,1,3],[3,1,null,null,2],[3,2,null,1]]
示例 2：
1
2
输入：n = 1
输出：[[1]]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
var generateTrees = function(n) {
  if(n===0){
    return []
  }
  return build(1, n)
};
function build(l, r){
  const res = []
  if(l>r){
    res.push(null)
    return res
  }
  for(var i=l;i<=r;i++){
    const leftTree = build(l, i-1)
    const rightTree = build(i+1, r)
    for(var left of leftTree){
      for(var right of rightTree){
        const root = new TreeNode(i, left, right)
        res.push(root)
      }
    }
  }
  return res
}