常见网页协议
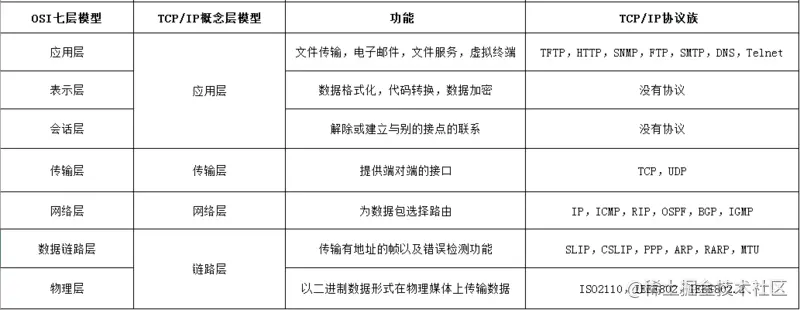
- TCP/IP 是互联网相关的各类协议族的总称
- IP(Internet Protocol)网际协议(网络层协议)IP 协议的作用是把各种数据包传送给对方。而要保证确实传送到对方那里,则需要满足各类条件。其中两个重要的条件是 IP 地址和 MAC 地址(Media Access Control Address)
- HTTP 超文本传输协议是一个用于传输超媒体文档(例如 HTML)的应用层协议。它是为 Web 浏览器与 Web 服务器之间的通信而设计的,但也可以用于其他目的
- TCP(Transmission Control Protocol,传输控制协议)是一种面向连接的、可靠的、基于字节流的传输层通信协议
- UDP(User Data Protocol,用户数据报协议)一个非连接的协议,传输数据之前源端和终端不建立连接, 当它想传送时就简单地去抓取来自应用程序的数据,并尽可能快地把它扔到网络上
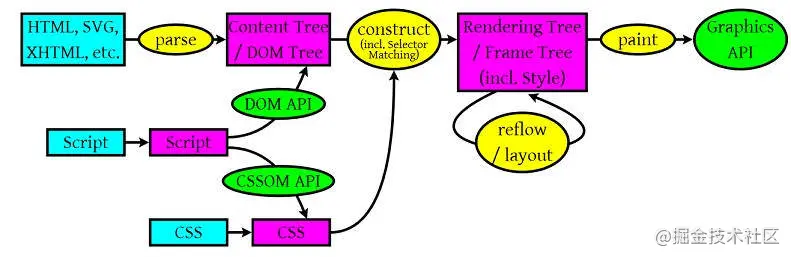
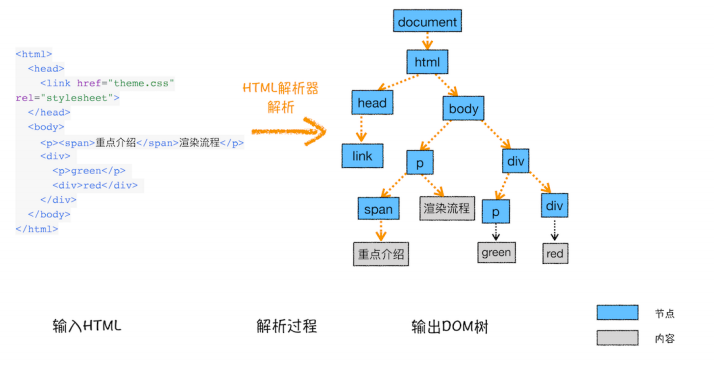
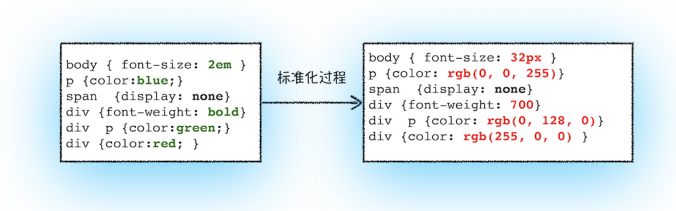
TCP/IP 的分层管理
利用 TCP/IP 协议族进行网络通信时,会通过分层顺序与对方进行通信
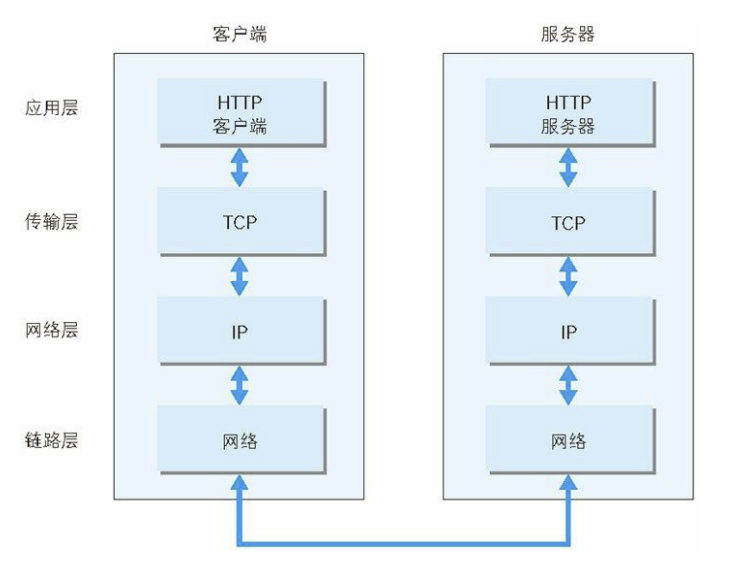
这些层基本上被分为4层:
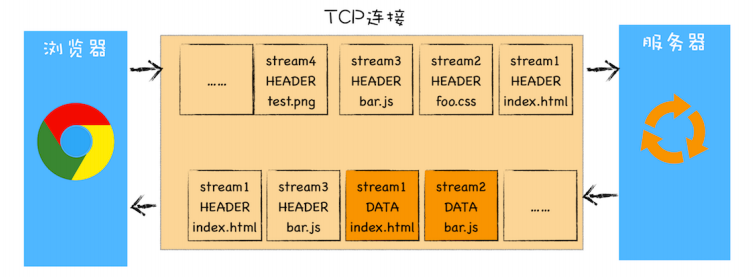
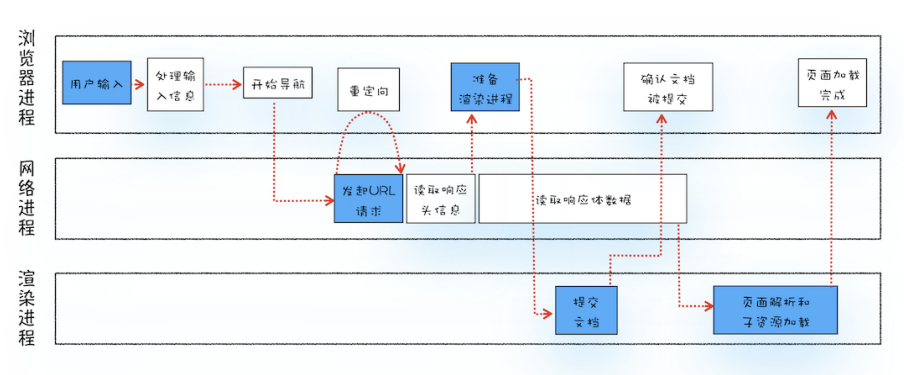
TCP/IP 通信传输流
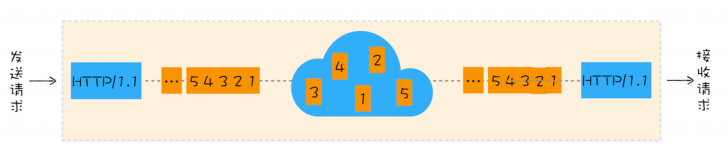
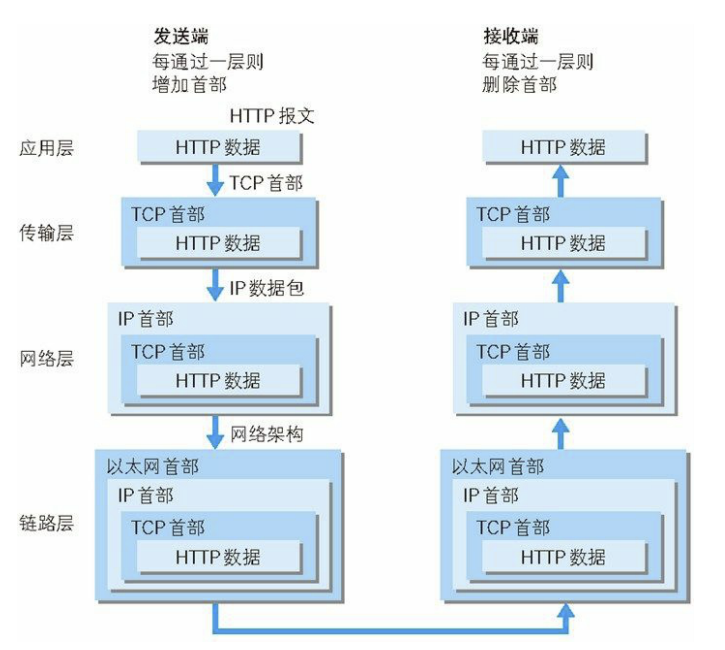
利用 TCP/IP 协议族进行网络通信时,会通过分层顺序与对方进行通信。发送端从应用层往下走,接收端则往应用层往上走。 发送端在层与层之间传输数据时,每经过一层时必定会被打上一个该层所属的首部信息。反之,接收端在层与层传输数据时,每经过一层时会把对应的首部消去。
这种把数据信息包装起来的做法称为封装(encapsulate),如下图所示
TCP
头部至少20个字节
待整理
TCP协议的特点
面向连接
面向连接,是指发送数据之前必须在两端建立连接。建立连接的方法是“三次握手”,这样能建立可靠的连接。建立连接,是为数据的可靠传输打下了基础。
仅支持单播传输
每条TCP传输连接只能有两个端点,只能进行点对点的数据传输,不支持多播和广播传输方式。
面向字节流
TCP不像UDP一样那样一个个报文独立地传输,而是在不保留报文边界的情况下以字节流方式进行传输。
可靠传输
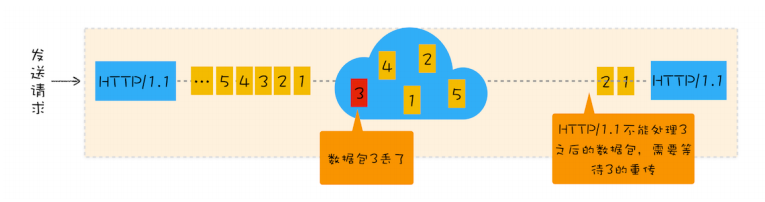
对于可靠传输,判断丢包,误码靠的是TCP的段编号以及确认号。TCP为了保证报文传输的可靠,就给每个包一个序号,同时序号也保证了传送到接收端实体的包的按序接收。然后接收端实体对已成功收到的字节发回一个相应的确认(ACK);如果发送端实体在合理的往返时延(RTT)内未收到确认,那么对应的数据(假设丢失了)将会被重传。
提供拥塞控制
当网络出现拥塞的时候,TCP能够减小向网络注入数据的速率和数量,缓解拥塞
TCP提供全双工通信
TCP允许通信双方的应用程序在任何时候都能发送数据,因为TCP连接的两端都设有缓存,用来临时存放双向通信的数据。当然,TCP可以立即发送一个数据段,也可以缓存一段时间以便一次发送更多的数据段(最大的数据段大小取决于MSS)
UDP
UDP协议全称是用户数据报协议,在网络中它与TCP协议一样用于处理数据包,是一种无连接的协议。在OSI模型中,在第四层——传输层,处于IP协议的上一层。UDP有不提供数据包分组、组装和不能对数据包进行排序的缺点,也就是说,当报文发送之后,是无法得知其是否安全完整到达的。
它有以下几个特点:
1. 面向无连接
首先 UDP 是不需要和 TCP一样在发送数据前进行三次握手建立连接的,想发数据就可以开始发送了。并且也只是数据报文的搬运工,不会对数据报文进行任何拆分和拼接操作。
具体来说就是:
- 在发送端,应用层将数据传递给传输层的 UDP 协议,UDP 只会给数据增加一个 UDP 头标识下是 UDP 协议,然后就传递给网络层了
- 在接收端,网络层将数据传递给传输层,UDP 只去除 IP 报文头就传递给应用层,不会任何拼接操作
2. 有单播,多播,广播的功能
UDP 不止支持一对一的传输方式,同样支持一对多,多对多,多对一的方式,也就是说 UDP 提供了单播,多播,广播的功能。
3. UDP是面向报文的
发送方的UDP对应用程序交下来的报文,在添加首部后就向下交付IP层。UDP对应用层交下来的报文,既不合并,也不拆分,而是保留这些报文的边界。因此,应用程序必须选择合适大小的报文
4. 不可靠性
首先不可靠性体现在无连接上,通信都不需要建立连接,想发就发,这样的情况肯定不可靠。
并且收到什么数据就传递什么数据,并且也不会备份数据,发送数据也不会关心对方是否已经正确接收到数据了。
再者网络环境时好时坏,但是 UDP 因为没有拥塞控制,一直会以恒定的速度发送数据。即使网络条件不好,也不会对发送速率进行调整。这样实现的弊端就是在网络条件不好的情况下可能会导致丢包,但是优点也很明显,在某些实时性要求高的场景(比如电话会议)就需要使用 UDP 而不是 TCP。
从上面的动态图可以得知,UDP只会把想发的数据报文一股脑的丢给对方,并不在意数据有无安全完整到达。
5. 头部开销小,传输数据报文时是很高效的

UDP 头部包含了以下几个数据:
- 两个十六位的端口号,分别为源端口(可选字段)和目标端口 (4字节?)
- 整个数据报文的长度
- 整个数据报文的检验和(IPv4 可选 字段),该字段用于发现头部信息和数据中的错误
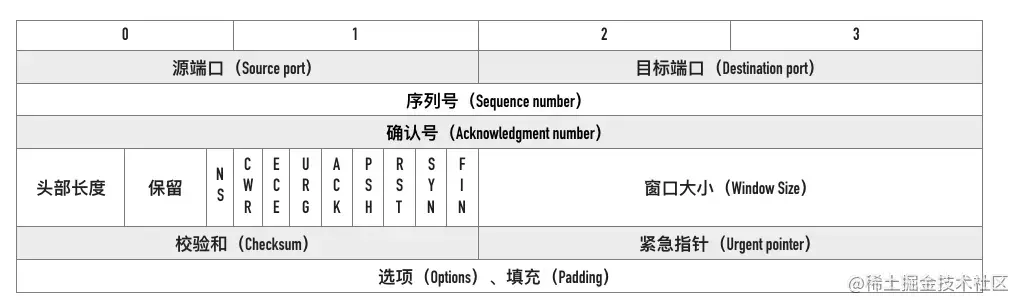
因此 UDP 的头部开销小,只有八字节,相比 TCP 的至少二十字节要少得多,在传输数据报文时是很高效的
TCP与UDP的区别
|
UDP |
TCP |
| 是否连接 |
无连接 |
面向连接 |
| 是否可靠 |
不可靠传输,不使用流量控制和拥塞控制 |
可靠传输,使用流量控制和拥塞控制 |
| 连接对象个数 |
支持一对一,一对多,多对一和多对多交互通信 |
只能是一对一通信 |
| 传输方式 |
面向报文 |
面向字节流 |
| 首部开销 |
首部开销小,仅8字节 |
首部最小20字节,最大60字节 |
| 适用场景 |
适用于实时应用(IP电话、视频会议、直播等) |
适用于要求可靠传输的应用,例如文件传输 |
TCP 拥塞控制
拥塞处理和流量控制不同,后者是作用于接收方,保证接收方来得及接受数据。而前者是作用于网络,防止过多的数据拥塞网络,避免出现网络负载过大的情况。
拥塞处理包括了四个算法,分别为:慢开始,拥塞避免,快速重传,快速恢复。
慢开始算法
慢开始算法,顾名思义,就是在传输开始时将发送窗口慢慢指数级扩大,从而避免一开始就传输大量数据导致网络拥塞。
慢开始算法步骤具体如下
- 连接初始设置拥塞窗口(Congestion Window) 为 1 MSS(一个分段的最大数据量)
- 每过一个 RTT 就将窗口大小乘二
- 指数级增长肯定不能没有限制的,所以有一个阈值限制,当窗口大小大于阈值时就会启动拥塞避免算法。
拥塞避免算法
拥塞避免算法相比简单点,每过一个 RTT 窗口大小只加一,这样能够避免指数级增长导致网络拥塞,慢慢将大小调整到最佳值。
在传输过程中可能定时器超时的情况,这时候 TCP 会认为网络拥塞了,会马上进行以下步骤:
- 将阈值设为当前拥塞窗口的一半
- 将拥塞窗口设为 1 MSS
- 启动拥塞避免算法
快速重传
快速重传一般和快恢复一起出现。一旦接收端收到的报文出现失序的情况,接收端只会回复最后一个顺序正确的报文序号(没有 Sack 的情况下)。如果收到三个重复的 ACK,无需等待定时器超时再重发而是启动快速重传。具体算法分为两种:
TCP Taho 实现如下
- 将阈值设为当前拥塞窗口的一半
- 将拥塞窗口设为 1 MSS
- 重新开始慢开始算法
TCP Reno 实现如下
- 拥塞窗口减半
- 将阈值设为当前拥塞窗口
- 进入快恢复阶段(重发对端需要的包,一旦收到一个新的 ACK 答复就退出该阶段)
- 使用拥塞避免算法
TCP New Ren 改进后的快恢复
TCP New Reno 算法改进了之前 TCP Reno 算法的缺陷。在之前,快恢复中只要收到一个新的 ACK 包,就会退出快恢复。
在 TCP New Reno 中,TCP 发送方先记下三个重复 ACK 的分段的最大序号。
假如我有一个分段数据是 1 ~ 10 这十个序号的报文,其中丢失了序号为 3 和 7 的报文,那么该分段的最大序号就是 10。发送端只会收到 ACK 序号为 3 的应答。这时候重发序号为 3 的报文,接收方顺利接收并会发送 ACK 序号为 7 的应答。这时候 TCP 知道对端是有多个包未收到,会继续发送序号为 7 的报文,接收方顺利接收并会发送 ACK 序号为 11 的应答,这时发送端认为这个分段接收端已经顺利接收,接下来会退出快恢复阶段。